Posted On: Thursday - July 2nd 2020 7:28PM MST
In Topics: Genderbenders Websites Humor Political Correctness
If you're not a geek, it's not that you couldn't understand, but just that you don't WANT TO understand.
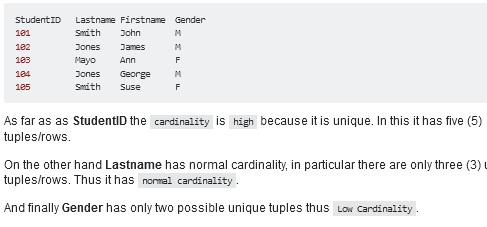
Stack Overflow is a very good website for searching for solutions to software questions. The graphic above is a screenshot of something that was part of the solution to a minor database question that came up regarding this site. I ought to right a quick post sometime about my appreciation for the folks that come on forum or Q/A sites, or make youtube videos, just to help others out.
Sure, sometimes on youtube, the idea is to eventually "monetize" that knowledge, and some of the help sites are designed to get revenue somehow. Many people, though, just want to help out on what may have been a frustrating project (such as car repair, or a software-related stumbling block, and they want the viewers/readers to not have to go through it. Thanks to all of you! I have not returned the favor yet.
I notice lots of times that the answer to my question was written years ago. That is REALLY bad when you have a follow-up question or think the solution is probably right, but you're missing something. It ain't like the guy will come right back on, awaiting questions from people like you. He could be long dead.
Well the screenshot above is from a simple answer, really a tutorial, with an example and everything - very nice. The example given of a column with a low cardinality, meaning there is only a small range of data that can be in it, is the Gender column of this example table. OK, I get it, so let's see ... Uh, oh, I want to learn, but then I don't want to be politically incorrect and shit... should I even be reading this?? OMG! It says right there "And finally Gender has only two possible unique tuples* thus [Low Cardinality]." What'd it just say? I think I'm gonna be sick.
Two Genders?!! In the words of cis-gendered* Butch Cassidy, in conversation with the Sundance Kid, "who ARE these guys?!" I can't even ... remember, oh yeah, they were the Regulators... in the movie. This ain't about movies, this is serious - there are many genders, there are many genders, your dBase column is unsound, there are many genders, there are many genders, there's no place like home. Toto, let's get the hell out of Kansas, this database, and StackOverFlow, for that matter.
Now this is the problem with old information. It may help some computer geek somewhere, but it could also have very outdated, un-Politically Correct data too. StackOverFlow has overflown the PC stack. This is egregious and deserves a thousand mean tweets and a protest. I think it's time to put the hurt on StackOverFlow.com.
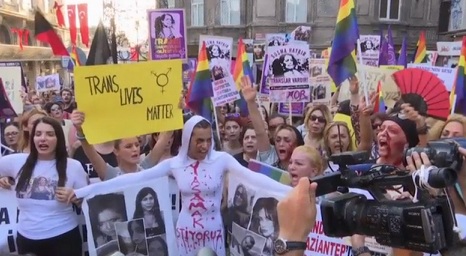
You'd better damn well find another site to answer your software questions, geeks, because, if this gets out, they ain't long for this internet.
----------/----####----//--H--***-- .. ey, I can type again. Whewww! Sorry, readers that was the dark side of Peak Stupidity. Now that he's been conquered and relegated to the mirrored site on our server in San Francisco, everything is back to normal.
Here's the best take I've heard on the multiple gender question, and there's probably a best-selling book too:
Men are from Mars, women are from Venus. All the other recently invented genders are from Uranus.
PS: That was some real serendipity. I had saved that line in a Notepad file months ago and just happened to look at it right before I wrote this post.
* Don't ask. I dunno. I didn't need to know, but I think I get it in context - 2 possible values?
Comments:
Bill H
Saturday - July 4th 2020 8:17AM MST
PS Yeah, doesn't matter. With today's systems a bit field now actually slows comparison down, because it has to run the comparison through something called a "bit mask" to make the comparison. It's a bit complicated, but in oversimplified terms, computer systems no longer look at individual bits.
Moderator
Friday - July 3rd 2020 7:31PM MST
PS: That makes sense, Mr. Blanc. I would imagine this applies for databases in general. I made fun of "the geeks" in this post, but one can really get into this stuff. I learned most of it informally, and unfortunately only for exactly what I needed to know at the moment.
Moderator
Friday - July 3rd 2020 7:29PM MST
PS: Bill, yes I understand the difference, which explains why variables in the old FORTRAN (and plenty of other languages) of the past made a distinction between types of variables. A binary is indeed cheap to store, and that MATTERED by in the day, a lot more.
Haha, it would be funny if some WOKE-ASS coder or manager decided that, no indeed, GENDER (no more than 8 Chars in FORTRAN, mind you) must not be a binary variable anywhere in the software, causing extra computation time*.
* But, I think, as powerful as computers are now, maybe nobody cares about this. You tell me.
Haha, it would be funny if some WOKE-ASS coder or manager decided that, no indeed, GENDER (no more than 8 Chars in FORTRAN, mind you) must not be a binary variable anywhere in the software, causing extra computation time*.
* But, I think, as powerful as computers are now, maybe nobody cares about this. You tell me.
MBlanc46
Friday - July 3rd 2020 2:36PM MST
PS Looks like a figure from my book on Access.
Bill H
Friday - July 3rd 2020 10:42AM MST
PS There is a type of field in a relational database called a "bit" field, because it is allocated one "bit, which is one eighth of a "byte." A "bit" can contain only a 1 or a 0, and is most often often used for "yes/no" type data, such as 1 for alive and 0 for dead.
The bit field is often used for the gender column as well: 1 for male, usually and 0 for female. (Don't start on me, I didn't design that protocol.)
The advantage of using a bit field is that the computer can compare between single bits in separate records a lot faster than it can for bytes, numbers (which have lots of bytes) or (gasp) alphabetic strings. The speed difference between comparing a bit and even a single byte is enormous.
I have no idea what good it does for you to know any of this, other than to know that this multiple gender nonsense might be making it take longer for you to get information on anything from anybody who needs to search a database to give you the information you need.
The bit field is often used for the gender column as well: 1 for male, usually and 0 for female. (Don't start on me, I didn't design that protocol.)
The advantage of using a bit field is that the computer can compare between single bits in separate records a lot faster than it can for bytes, numbers (which have lots of bytes) or (gasp) alphabetic strings. The speed difference between comparing a bit and even a single byte is enormous.
I have no idea what good it does for you to know any of this, other than to know that this multiple gender nonsense might be making it take longer for you to get information on anything from anybody who needs to search a database to give you the information you need.